運動量保存則
概要
一般に、質量
式で表すと、時刻
が成立する。これを運動量保存則という。ベクトルが出てきて、じんましんができる方も多いと思うが、導出や使い方が大事なので、このあとゆっくり確認しよう。

初めにちょっと退屈な、でも正確な理解には欠かせない用語の話をしよう。このように物体をまとめて考えるときに、まとめたものを物体系といい、物体系の内部で及ぼしあう力を内力、物体系の外から物体系の中の物体にはたらく力を外力という。
物体系の取り方は自分次第であり、何を物体系と見るかによって、ある力が内力なのか外力なのかが決まる。例えば上の
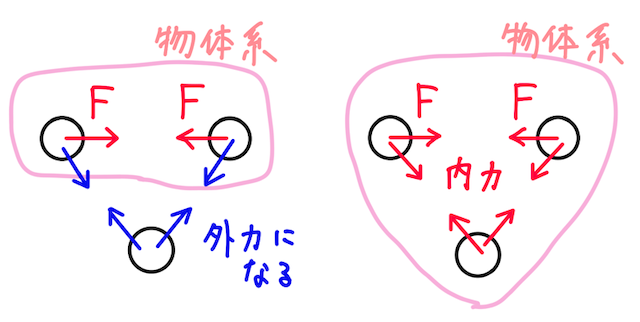
上の運動量保存則の式で「あれ?でも重力はたらくから外力の力積は
上の例では仮想的な一般例を考えたものの、実際問題では、確かに
どうしてくれるんだ?という気持ちになるが、実はこの運動量保存則はベクトルの式(運動量がベクトル量であることに注意!)なので、成分ごとに考えることができ、運動量保存則が成り立つかどうか、つまり外力の力積が
つまり、鉛直方向には確かに外力である重力の力積が存在するが、一方で水平方向には内力しかはたらいていないので、水平方向では運動量保存則が成り立つ。水平方向に
が成り立つ。
例
【問】滑らかな水平面の床の上に、質量
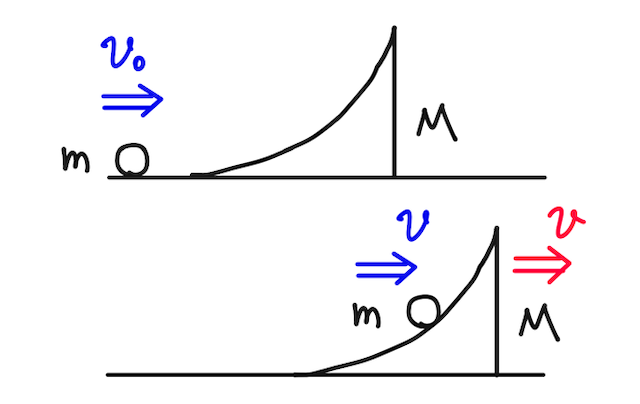
【答】小球にはたらく力は、重力と台からの垂直抗力のみ。台にはたらく力は、重力と小球からの垂直抗力と床からの垂直抗力のみ。(まずはしっかり力を把握!!)
小球と台を1つの物体系と考えると、水平方向には小球と物体間の垂直抗力しかはたらいておらず、それは内力である。

よって、小球と台の水平方向の運動量の和は保存する。小球が台上の最高点に達したときの、小球および台の速さを
と求められる。イメージでこの答えが合ってそうかを確認すると、確かに、
このように 「極端なケースを考えて、答えが合ってそうか確認する」 のは、物理の問題でとても役に立つので、オススメ。
あと、斜面が急であっても緩やかであっても上の議論は変わらないというのが、隠れおもしろポイント。
導出
まずは力が時間によらず一定の場合を考えてみよう (基礎編)。
質量
このとき、
そこで、それぞれの物体について、運動量変化と力積の関係より、
となるので、両辺足すと、
となって、運動量保存則の式が導かれる。
では発展編として、力が一定ではない場合を考える(上の基礎編で理解しておけば、理工系に進まない限り十分に生きていけるはずなので、飛ばしてもらっても問題はないです)。よくわからない! という方は、化学好きな東工大生・かずきさんの動画がオススメ。
時間
ベクトルのまま計算すると、積分などがややこしく見えるので、まず
とおく(各成分は
となる。さらに、速度の
となる。両辺足すと、
となり、運動量保存則の
が示されるので、ベクトルの形にまとめて
が成り立つ。
補足
運動量保存則は実は物体が
余談になるが、問題を解く上で運動量保存則をはじめとする保存則を用いるメリットは何だろうか?それは、
今回の例題のように、物体にはたらく水平方向の力が刻一刻と変わり、運動方程式から位置や速度などを時間の関数として完璧に求めるのが難しい運動でも、保存則を用いれば、ある時点での位置や速度の情報が求められるというのが、保存則のすごいところ!
